Skip to main content

endeav: a course on code efficiency and software development with R

5 Rcpp or how to easily embed C++ code into a package

Rcpp (“R-C-Plus-Plus”) is a package which facilitates the interface between C++ and . is an interpreted language, a feature that makes a number of things easy (including giving us access to the console in which we can evaluate code and variables on the fly). Nevertheless, this ease of use is counterbalanced by larger computation times compared to lower level languages such as C, Fortran and C++ (but which require compilation).

The curious reader is directed towards the online book Rcpp for everyone by Masaki E. Tsuda, which is a very thorough and complete resource for understanding how to use Rcpp, in complement to the introduction that can be found in the “Rcpp” section of Hadley Wickham’s book Advanced R3.

5.1 First function in Rcpp

👉 Your turn !

  1. To make your package ready for use with Rcpp, start by running the following command:

    usethis::use_rcpp()

  2. See the changes made

  3. You should also add the following 2 Roxygen comments in the general help page of the package, as indicated in the console:

    #' @useDynLib mypkgr
#' @importFrom Rcpp sourceCpp, .registration = TRUE
NULL

We are now going to create a first function in Rcpp to invert a matrix. For this, we will use the C++ library Armadillo. It is a modern and simple linear algebra library, highly optimized, and interfaced with via the RcppArmadillo package.

C++ is not a very different language from . The main differences that will have an impact for us:

  • C++ is very efficient for for loops (including nested for loops – ⚠️ there is often one order that is faster than the other, due to the way C++ allocates and walks through memory).

  • Each command must end with a semicolon ;.

  • C++ is a typed language: you must declare the type of each variable before you can use it in the code.

👉 Your turn !

  1. Create a new C++ file from RStudio (via the File > New File > C++ File menu), and save it in the src folder. Take the time to read it and try to understand each line.
  2. Compile and load your package (via the “Install and Restart” button) and try using the timesTwo() function from the console.
  3. Install the RcppArmadillo 👉 package, and don’t forget to make the necessary additions to DESCRIPTION (use usethis::use_rcpp_armadillo())
  4. Using Hadley Wickham’s introduction to Rcpp in his book Advanced R, as well as the documentation for the RcppArmadillo package and for the C++ library Armadillo, try to write a short function invC() in C++ that computes the inverse of a matrix.
  5. When you have successfully compiled your invC function and it is accessible from , create a mvnpdf_invC() function from the mvnpdfsmart implementation replacing only the matrix inverse calculations with a call to invC.
  6. Evaluate the performance gain of this new implementation mvnpdf_invC.
n <- 1000
mb <- microbenchmark(mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2)),
                     mvnpdf(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfsmart(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfoptim(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdf_invC(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     times=100L)
mb
## Unit: microseconds
##                                                            expr      min
##              mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2))   26.363
##       mvnpdf(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 1678.868
##  mvnpdfsmart(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 1156.036
##  mvnpdfoptim(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)  670.104
##  mvnpdf_invC(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE) 1146.934
##        lq       mean   median        uq      max neval
##    55.391   68.27074   66.625   82.7175  154.939   100
##  1787.313 1941.00519 1885.242 1989.9145 4067.651   100
##  1221.677 1320.32505 1261.139 1299.5155 3464.090   100
##   712.129  792.31475  727.914  746.3845 3080.002   100
##  1226.023 1362.15079 1269.421 1305.4400 3827.678   100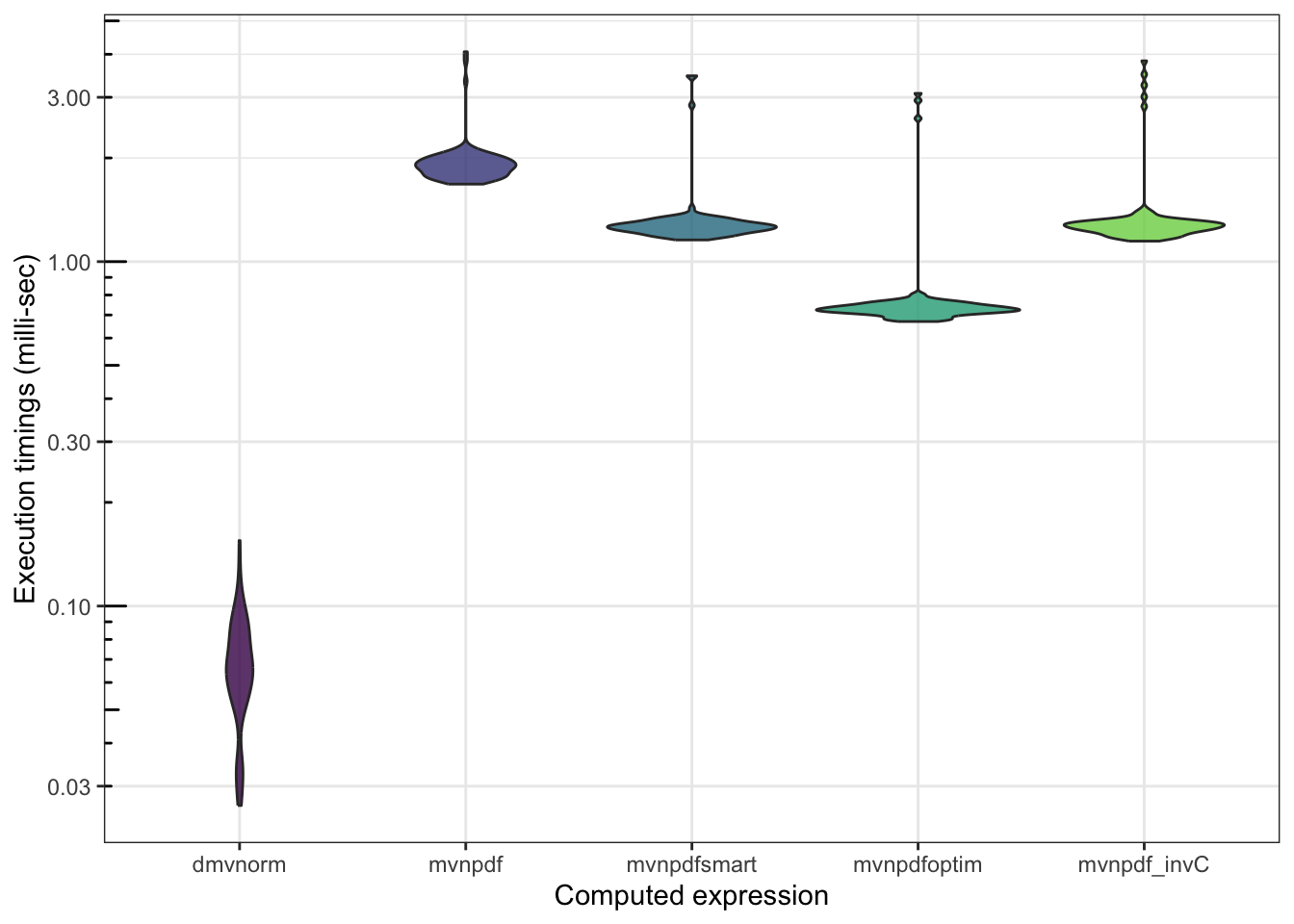

5.2 Optimize thanks to C++

As a general rule, not much computational time is gained by replacing an optimized function with a C++ function. Indeed, most of the base functions are in fact already wrappers around well optimized C or Fortran routines. The gain is then limited to the suppression of argument checking and type management (which is there for a reason!).

👉 Your turn !

  1. From mvnpdfsmart, propose a complete implementation in C++ for computating the density of the multivariate Normal distribution mvnpdfsmartC().

  2. Evaluate the performance gain of this new implementation mvnpdfsmartC.

You can download our proposal for mvnpdfsmartC.cpp here.

For (relatively small) additional speed gain (at the cost of code readability!), you can have a look at our optimized Armadillo C++ implementation in mvnpdfoptimC.cpp.

Finally, we asked LeChat from Mistral AI to propose improvements over this last mvnpdfoptimC() function and it delivered an additional few microseconds speedup implemented in mvnpdfC_LeChat.cpp.

n <- 1000
mb <- microbenchmark(mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2)),
                     mvnpdf(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfsmart(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfoptim(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdf_invC(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
                     mvnpdfsmartC(x=matrix(1.96, nrow = 2, ncol = n), mean = rep(0, 2), varcovM = diag(2), Log=FALSE),
                     mvnpdfoptimC(x=matrix(1.96, nrow = 2, ncol = n), mean = rep(0, 2), varcovM = diag(2), Log=FALSE),
                     mvnpdfC_LeChat(x=matrix(1.96, nrow = 2, ncol = n), mean = rep(0, 2), varcovM = diag(2), Log=FALSE),
                     times=100L)
mb
## Unit: microseconds
##                                                                                                         expr
##                                                           mvtnorm::dmvnorm(matrix(1.96, nrow = n, ncol = 2))
##                                                    mvnpdf(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##                                               mvnpdfsmart(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##                                               mvnpdfoptim(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##                                               mvnpdf_invC(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
##    mvnpdfsmartC(x = matrix(1.96, nrow = 2, ncol = n), mean = rep(0,      2), varcovM = diag(2), Log = FALSE)
##    mvnpdfoptimC(x = matrix(1.96, nrow = 2, ncol = n), mean = rep(0,      2), varcovM = diag(2), Log = FALSE)
##  mvnpdfC_LeChat(x = matrix(1.96, nrow = 2, ncol = n), mean = rep(0,      2), varcovM = diag(2), Log = FALSE)
##       min        lq       mean    median        uq      max neval
##    24.231   53.7305   69.04687   65.6615   81.1390  231.240   100
##  1604.740 1781.5115 1952.24083 1883.4170 1986.0400 4263.508   100
##  1146.606 1221.7385 1323.93387 1273.2345 1313.9885 3622.350   100
##   665.840  706.3685  737.18656  739.8450  755.4045  932.012   100
##  1151.280 1202.4480 1390.74747 1261.7955 1310.7495 3727.720   100
##    33.497   35.6085   38.98321   38.1095   41.0205   76.014   100
##    18.204   20.1925   23.48234   21.4635   23.4725  144.607   100
##    14.596   16.7895   18.60129   17.7735   19.4955   36.572   100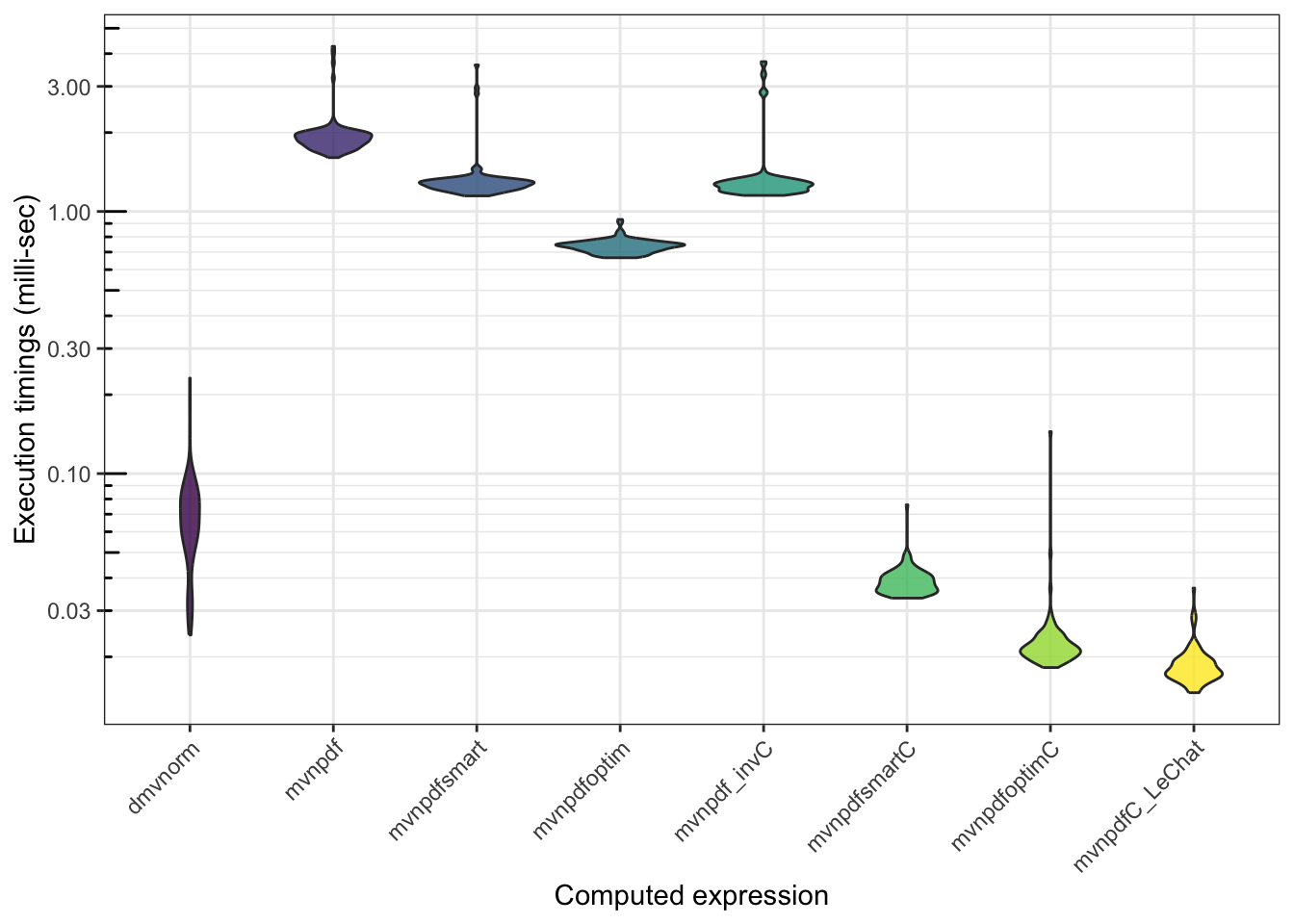

Note that Rcpp functions can be used outside of a package architecture thanks to the Rcpp::sourceCpp() function. But, as we have seen that it is always desirable to manage all of one’s code inside a package, it is unlikely that you will need this !

Annexe 5.1: premature optimization is a bad idea

Chambers, Software for Data Analysis: Programming with R, Springer, 2008:

“Including additional C code is a serious step, with some added dangers and often a substantial amount of programming and debugging required. You should have a good reason.”