6 R code Parallelization
6.1 Introduction to parallel execution in
Apart from optimizing the code and the algorithms, another way to get a high performing code is to take advantage of the parallel architectures of modern computers. The goal is then to parallelize one’s code in order to perform simultaneous operations on distinct parts of the same problem, using different computing cores. This does not reduce the total computation time needed, but the set of operations is executed faster, resulting in overall user speed-up.
There is a significant number of algorithms that are so-called “embarrassingly parallel”, i.e. whose computations can be broken down into several independent sub-computations. In statistics, it is often easy and straightforward to parallelize according to different observations or different dimensions. Typically, these are operations that can be written in the form of a loop whose operations are independent from one iteration to the next.
The necessary operations to execute code in parallel are as follows:
Start \(m\) “worker” processes (i.e. computing cores) and initialize them
Send the necessary functions and data for each task to the workers
Split the tasks into \(m\) operations of similar size and send them to the workers
Wait for all workers to finish their calculations
Collect the results from the different workers
Stop the worker processes
Depending on the platform, several communication protocols are available between the cores. Under UNIX systems, the Fork protocol is the most used (it has the benefit of sharing memory), but it is not available under Windows where the PSOCK protocol is used instead (with duplicated memory). Finally, for distributed computing architecture where the cores are not necessarily on the same physical processor, the MPI protocol is generally used. The advantage of the future and future.apply package is that the same code can be executed whatever the hardware configuration.
Since R 2.14.0, the parallel package is directly included in and allows to start and stop a cluster of several worker processes (step 1 and 6). In addition to the parallel package, we will use the future package which allows to manage the worker processes and the communication and articulation with the future.apply package, which in turn allows to manage the dialogue with the workers (sending, receiving and collecting the results – steps 2, 3, 4 and 5).
NB: the free plan on Posit Cloud only includes 1 core.
6.2 First parallel function
👉 Your turn !
Start by writing a simple function that computes the logarithm of \(n\) numbers:
Determine how many cores are available on your computer with the function
future::availableCores()(under Linux, preferparallel::detectCores(logical=FALSE)to avoid overthreading).Using the function
future::plan(multisession(workers = XX)), declare a “plan” of parallel computations on your computer (taking care to always leave at least one core available to handle other processes).Using one of the *apply functions
future.apply::future_*apply(), compute the log of \(n\) numbers in parallel and concatenate the results into a vector.Compare the execution time with that of a sequential function on the first 100 integers, using the command :
microbenchmark(log_par(1:100), log_seq(1:100), times=10)
library(microbenchmark)
library(future.apply)
log_seq <- function(x){
# try this yourself (spoiler alert: it is quite long...):
# res <- numeric(length(x))
# for(i in 1:length(x)){
# res[i] <- log(x[i])
# }
# return(res)
return(log(x))
}
log_par <- function(x){
res <- future_sapply(1:length(x), FUN = function(i) {
log(x[i])
})
return(res)
}
plan(multisession(workers = 3))
mb <- microbenchmark(log_par(1:100), log_seq(1:100), times = 50)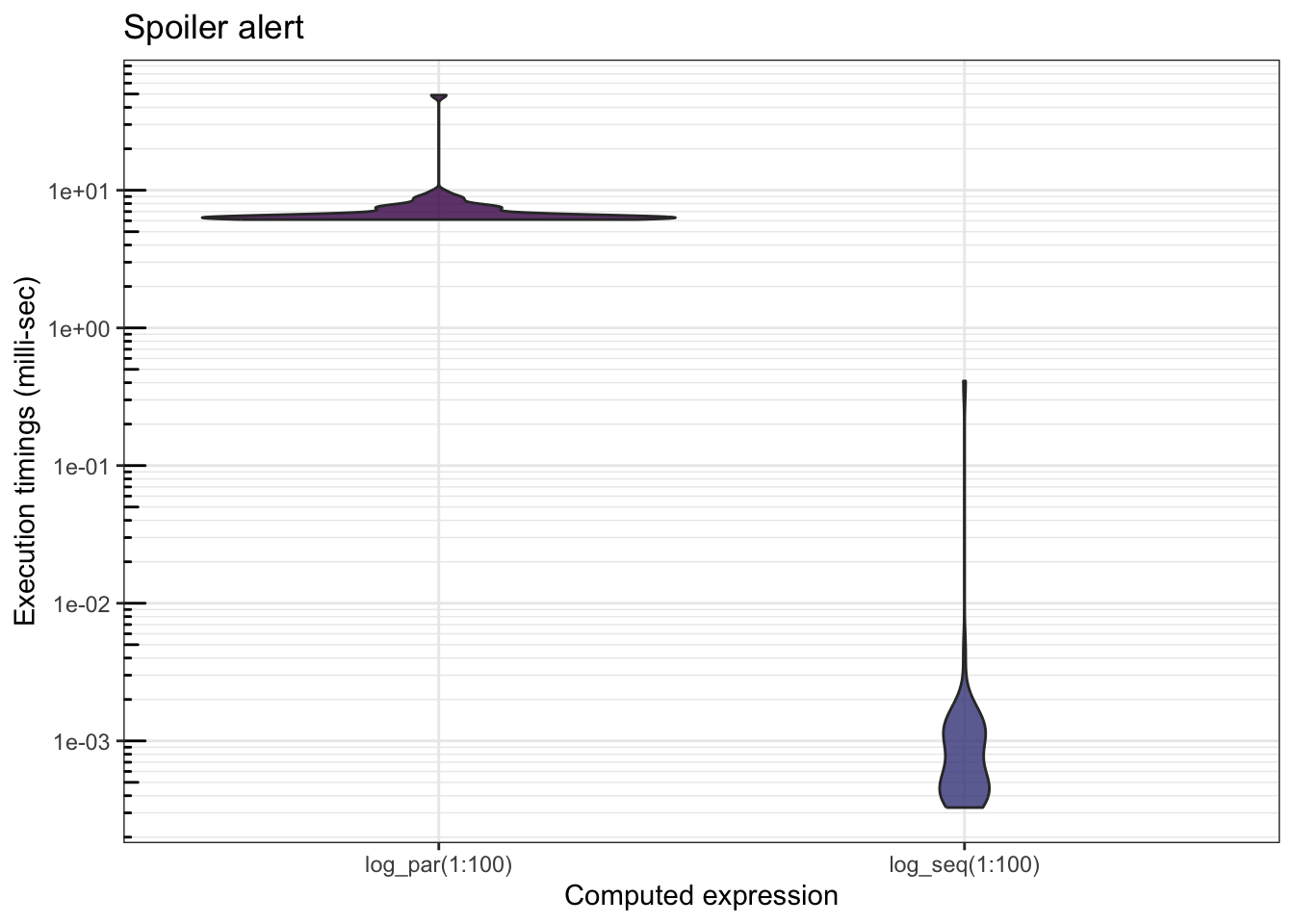
The parallel version runs much slower… Because in fact, if the individual tasks are too fast, will spend more time communicating with the cores than doing the actual computations.
A loop iteration must be relatively long for parallel computing to provide a significant gain in computation time!
By increasing \(n\), we observe a reduction in the difference between the 2 implementations (the parallel computation time increases very slowly compared to the increase of the sequential function).
6.3 Efficient parallelization
We will now look at another use case. Let’s say we have a large array of data with 10 observations for 100,000 variables (e.g. genetic measurements), and we want to compute the median for each of these variables.
## [1] 10 100000For an experienced user, such an operation is easily implemented using apply():
colmedian_apply <- function(x){
return(apply(X = x, MARGIN = 2, FUN = median))
}
system.time(colmedian_apply(x))## user system elapsed
## 1.612 0.003 1.615In reality, a (good) for loop is no slower – provided it is nicely programmed:
colmedian_for <- function(x){
p <- ncol(x)
ans <- numeric(p)
for (i in 1:p) {
ans[i] <- median(x[, i])
}
return(ans)
}
system.time(colmedian_for(x))## user system elapsed
## 1.470 0.001 1.473👉 Your turn ! Try to further improve this computation time by parallelizing your code for each of the 100,000 variables. Is there a gain in computation time?
colmedian_par <- function(x){
res <- future_sapply(1:ncol(x), FUN = function(i) {
median(x[, i])
})
return(res)
}
plan(multisession(workers = 3))
system.time(colmedian_par(x))## user system elapsed
## 0.126 0.018 0.872
mb <- microbenchmark(colmedian_apply(x),
colmedian_for(x),
colmedian_par(x),
times = 10)
mb## Unit: milliseconds
## expr min lq mean median uq max
## colmedian_apply(x) 1508.9948 1524.1869 1545.0013 1537.908 1559.9771 1609.639
## colmedian_for(x) 1448.6834 1463.6771 1504.0157 1493.679 1545.3759 1596.290
## colmedian_par(x) 690.3923 709.1447 751.2744 729.233 766.7742 871.308
## neval cld
## 10 a
## 10 a
## 10 b
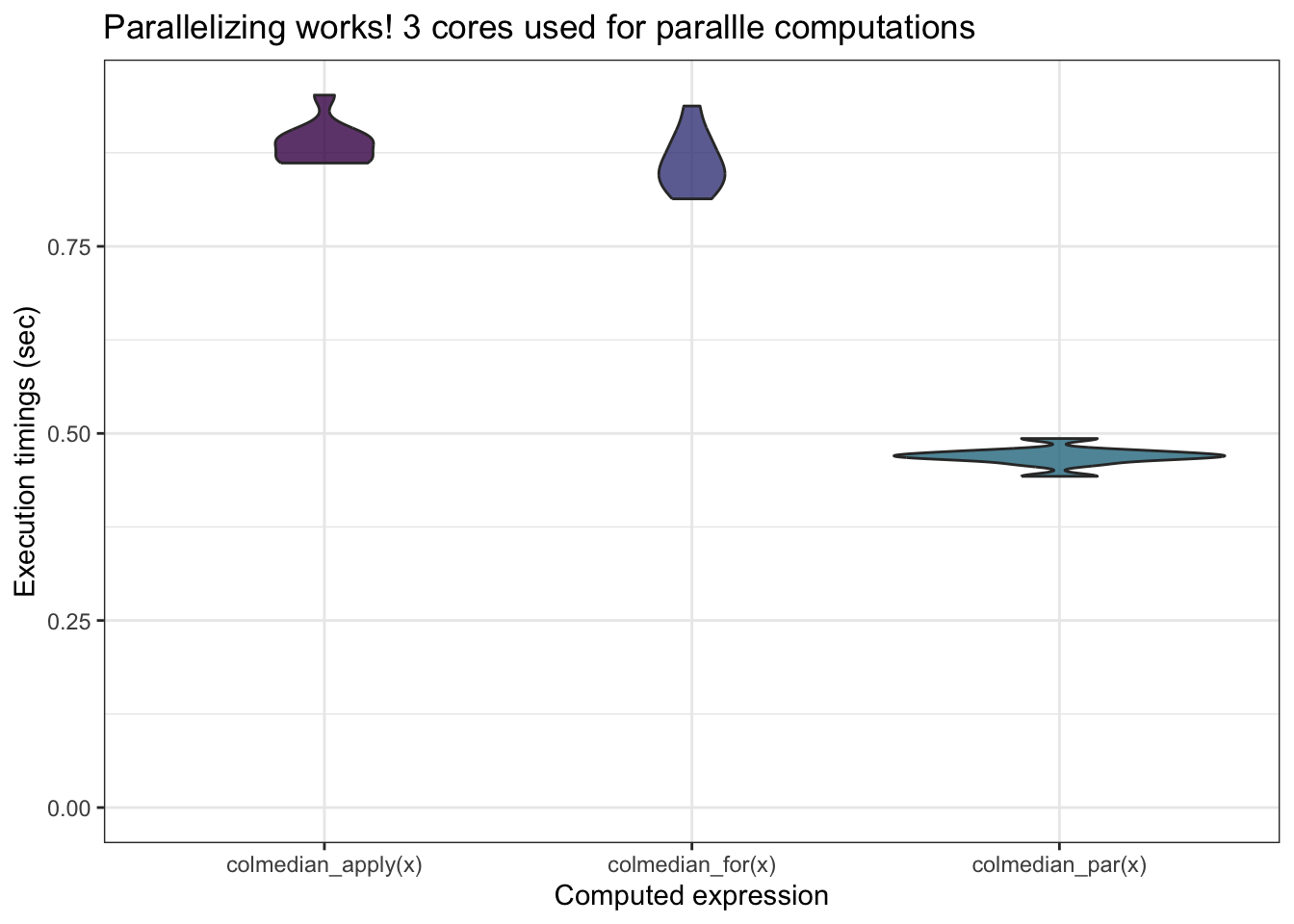
6.3.1 Other “plans” for parallel computations
To run your code (exactly the same code, this is one of the advantages of the future* family packages), you need to set up a “plan” of computations:
On a computer (or a single computer server) under Unix (Linux, Mac OS), you can use
plan(multicore(workers = XX))which is often more efficient. Themultisessionplan always works.on a HPC cluster (like CURTA in Bordeaux), we refer to the package
future.batchtools
6.4 Parallelization in our common theme example
👉 Your turn !
From the function
mvnpdfoptim()and/ormvnpdfsmart(), propose an implementation parallelizing the computations on the observations (columns of \(x\))Compare the execution times for 10 000 observations
plan(multisession(workers = 3))
n <- 10000
mb <- microbenchmark::microbenchmark(
mypkgr::mvnpdfsmart(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
mypkgr::mvnpdfsmart_par(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE),
times=20)
mb## Unit: milliseconds
## expr
## mypkgr::mvnpdfsmart(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
## mypkgr::mvnpdfsmart_par(x = matrix(1.96, nrow = 2, ncol = n), Log = FALSE)
## min lq mean median uq max neval cld
## 23.26963 23.62164 24.84931 24.16677 26.28758 26.68665 20 a
## 78.06261 88.34729 110.17293 91.34306 94.23536 487.86499 20 b
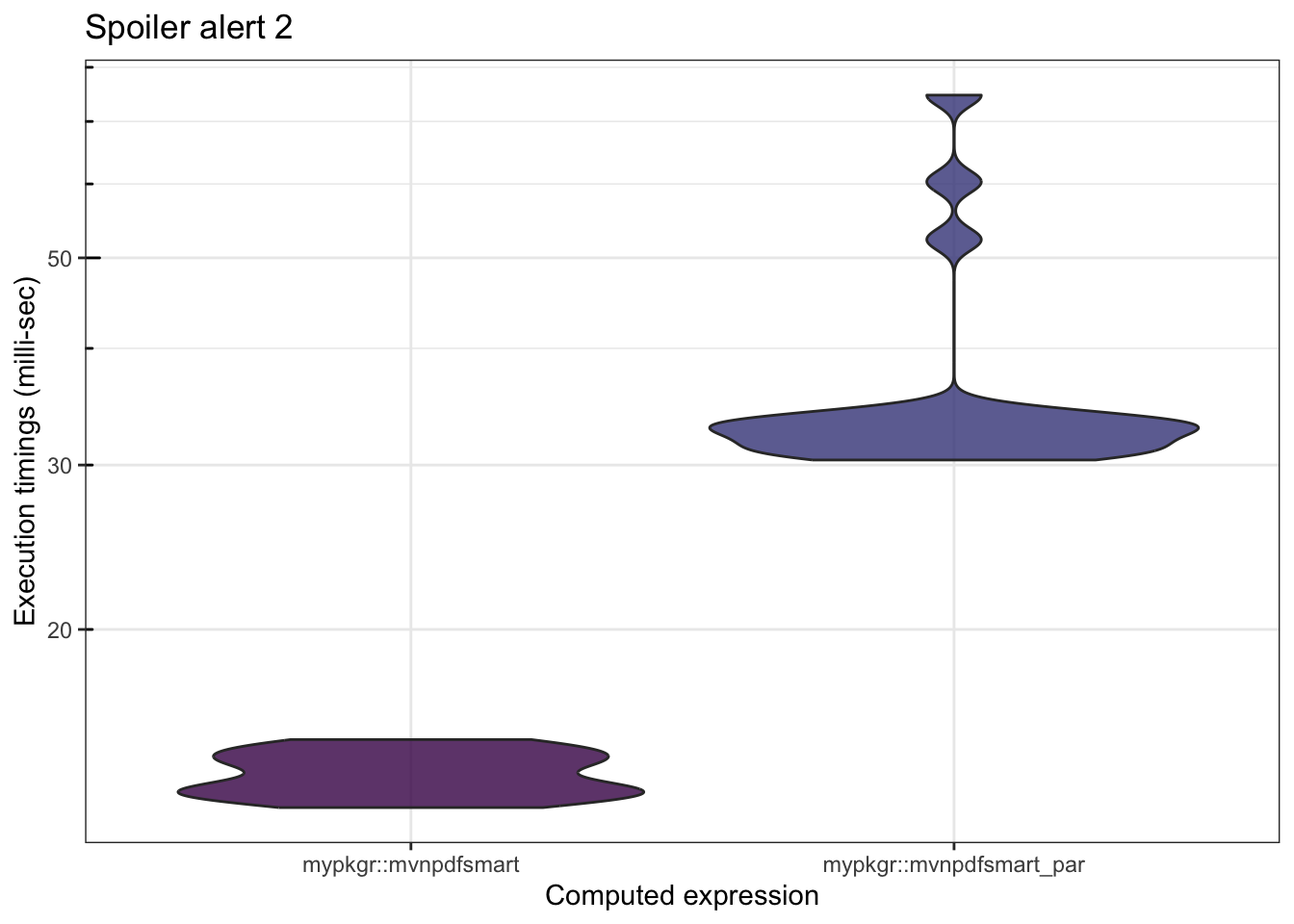
You can download our proposed implementation for mvnpdfsmart_par here.
In this example, the computation time of one iteration is really too fast for the parallel version to be efficient. We artificially add some time on each iteration to illustrate the gain of parallel computing for this example.
plan(multisession(workers = 3))
n <- 10000
system.time(mypkgr::mvnpdfsmart_sleepy(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE))## user system elapsed
## 0.355 0.123 13.616
system.time(mypkgr::mvnpdfsmart_sleepy_par(x=matrix(1.96, nrow = 2, ncol = n), Log=FALSE))## user system elapsed
## 0.324 0.014 5.223You can finally clone (or download or fork) our GitHub repository to get all the different implementations directly.